© 2024 EasyEDA Some rights reserved ISO/IEC
Editor Version
×
Standard


1.Easy to use and quick to get started
2.The process supports design scales of 300 devices or 1000 pads
3.Supports simple circuit simulation
4.For students, teachers, creators
Profession


1.Brand new interactions and interfaces
2.Smooth support for design sizes of over 5,000 devices or 10,000 pads
3.More rigorous design constraints, more standardized processes
4.For enterprises, more professional users
Ongoing
STD KM409 LC meter
License: Public Domain
Mode: Editors' pick
- 11
Update time:
2022-03-06 17:44:48
Creation time:
2018-11-28 15:34:37
Description







# A LOGIC IDEA #

# THANKS TO JLCPCB !!! #

# FINAL PRODUCT #

# L/C METER #
**Theory**
A capacitance + inductance they form a resonant circuit. He is vibrating. The frequency of vibrations depends on the capacity and inductance. When we add to the resonant LC circuit, the coil (in series to the coil) - or the capacitor (parallel to the capacitor), then the resonant frequency will decrease.
**Practice (resonant method)**
L/C circuit is cooperates with the LM393D comparator, from which the output is fed back loop to the LC circuit. Thanks to this, the vibrations do not expire. The comparator output also gives a rectangular signal to the input pin of the microcontroller. This signal has the resonance frequency of the LC circuit. The frequency of this signal is measured by the microcontroller.
Knowing the inductance values and capacities of the LC generator based on the frequency difference, we can calculate the value of the attached capacitance or inductance to the LC circuit.
**Used formulas**:
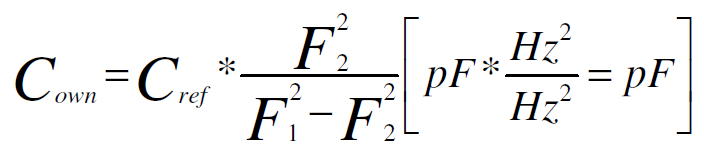
**Where:**
**Cown** – capacitance of LC circuit [pF]
**Cref** - a referential knowing value of capacitance which was added to LC circuit (generator) [pF]
**F1** – a resonant frequency of LC circuit **before** add Cref capacitor [Hz]
**F2** – a resonant frequency of LC circuit **after** add Cref capacitor [Hz]
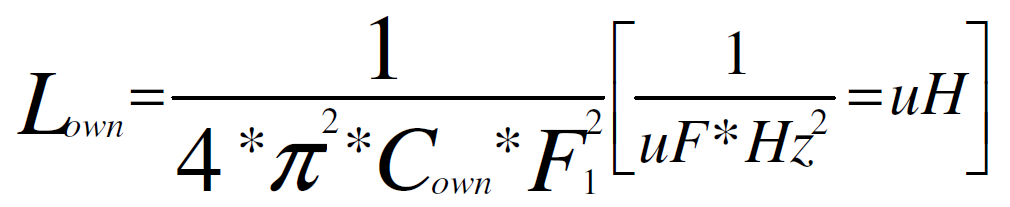
**Where:**
**Lown** – a own inductance of LC circuit (without added any other inductor) [uH]
**Cown** – a own capacitance of LC circuit (without added any other capacitor) [uF]
**F1** – a frequency of resonant LC circuit [Hz]
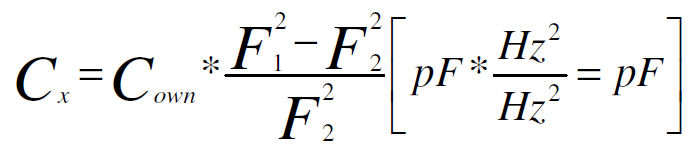
**Where:**
**Cx** - is a unknown value of capacitance which was added to LC circuit (generator) [pF]
**Cown** – a own capacitance of LC circuit [pF]
**F1** – a resonant frequency of LC circuit before add Cx capacitor [Hz]
**F2** – a resonant frequency of LC circuit after add Cx capacitor [Hz]
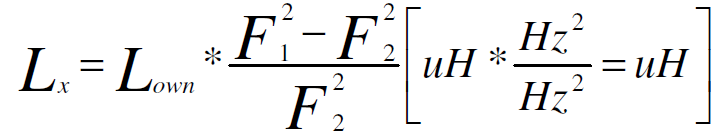
**Where:**
**Lx** - is a unknown value of inductance which was added to LC circuit (generator) [uH]
**Lown** – a own inductance of LC circuit [uH]
**F1** – a resonant frequency of LC circuit before add Lx inductor [Hz]
**F2** – a resonant frequency of LC circuit after add Lx inductor [Hz]
# MEASURE FOR BIGGER CAPACITORS - ELECTROLYTIC #
**Charging time to capacitance by constant voltage.**
When we charging capacitor by constant voltage we can observed a curve of charge:
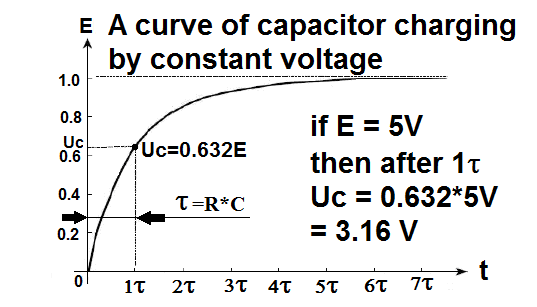
We can see the charging time if depend from resistance and capacitance. And these two values form a time constant called tau τ which units is the seconds [s]
So from above diagram we can get the known:
After one τ the voltage on the capacitor get the 0.632 E value
So if our E have 5V, after the τ time on the capacitor voltage will present 3.16V.
**AND FINALLY – when we charge the capacitor up to 0.632E, knowing the value of R and measuring the charging time, we can very easily calculate the capacity of the capacitor.**
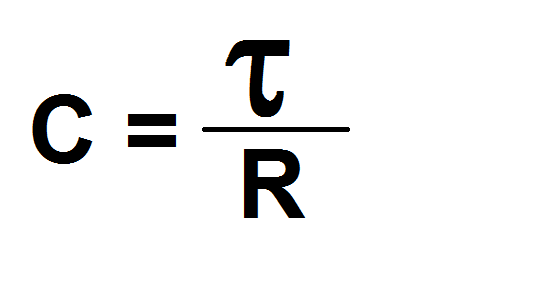
If we look at the diagram, notice that the capacitor can be charged by one or two parallel resistors RES1 and RES2.
Therefore, the program uses one more formula:
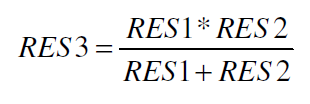
# WHAT YOU MUST DO TO GET A HIGH ACCURACY OF MEASUREMENT. #
Start with RES1 and RES3 soldering, and then measure and store their values. After assembling the whole and connecting the power supply, the VCC supply value should be measured, then the PR1 potentiometer should be set to 0.632 VCC at TP (arround 3.16V).
# The FIRMWARE #
Wrote in assembler in two options – for ATmega8A or ATmega328P – why 328P? Cause I got a few unused Arduino so I don’t need to purchase M8A
After power on we can see three screens:

Honestly, after the first power on third screen going to calibrate menu, which I’ll describe later.
After reset we can put capacitor into the socket and measure capacitance.
After pressed the left button we can see the L measure screen or the second one after put inductor into the **left socket**.

Next one press the left button invoke the third menu for CE measure:
In the **right socket** we can do measure of electrolytic capacitors.

After this, the left button go back to small capacitors measure menu.
Al the time by press right button we can invoke 7 specials menu. In this mode the right button select menu, and after the select any one by pressing left button execute it and go inside.
How the program calculate capacitance:
1. Simply start charge of the capacitor and counting the clocks edges.
2. After charging capacitor program multiply by 125 value of counted clock edges, cause crystal have 8MHZ for translate to decimal relation to seconds. And divide by 10.
3. After that value is divided by RES2*100 (for better precision) or by RES3 (two parallely connected resistors RES3=RES1*RES2/[RES1+RES2] ) – result in [uF] or in 0.01 [uF]
# MEASURE MENU #
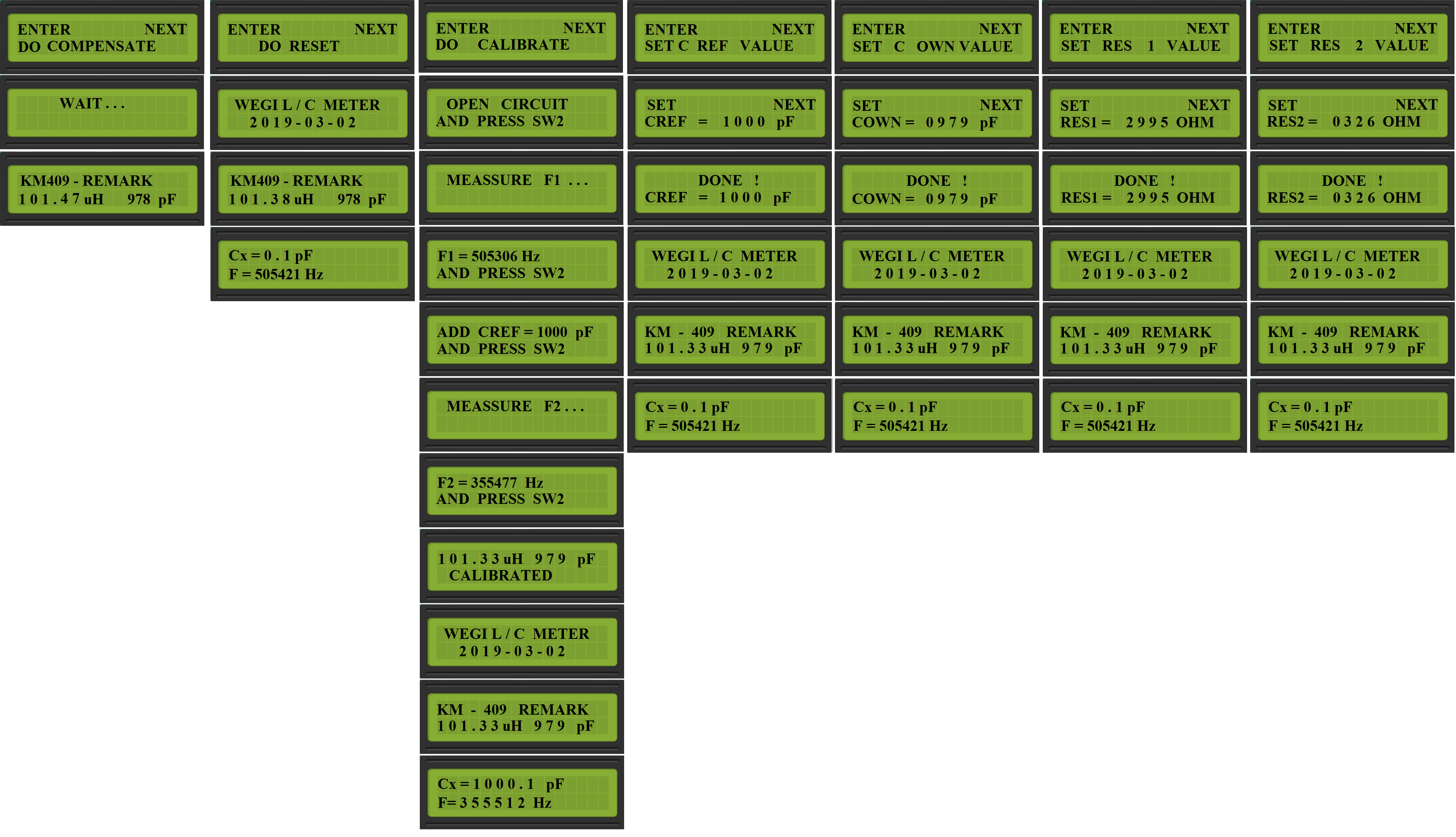
# MENU COMPENSATE: #
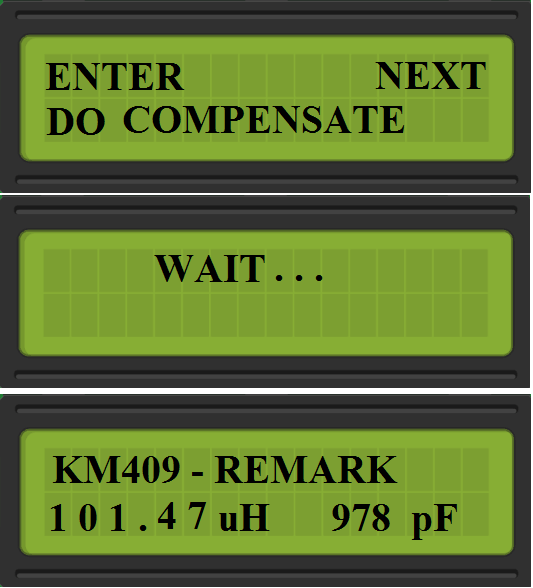
After select his menu program compensate the frequency value, which can be a bit floating depend from thermical values. And go back to last used menu of measure.
# MENU RESET: #
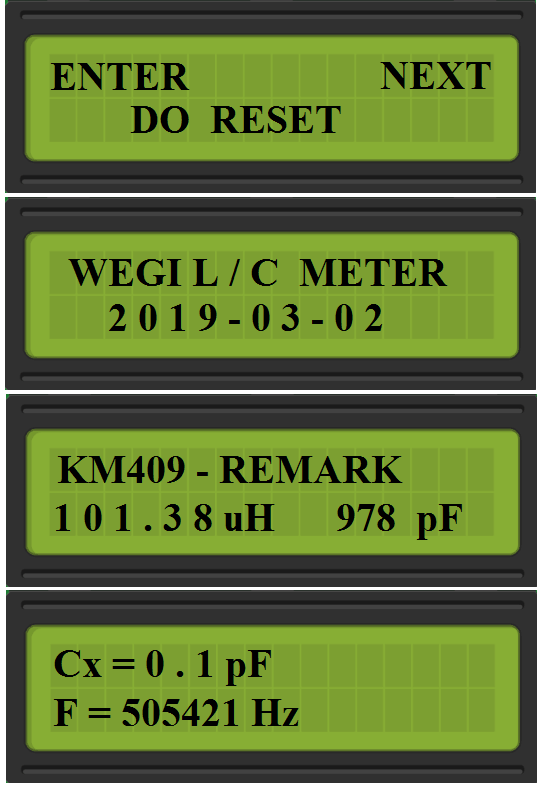
Simply restart of firmware, and lose the compensate value.
# MENU CALIBRATE: #

Most probably don’t need describe this menu, everything is on the following step by step screens.
Note: You can choose in the next menu the reference value of the calibrate capacitor, which you’ll use.
# MENU SET REF VALUE # – you can change the referential value your cap. for calibrate if you need.

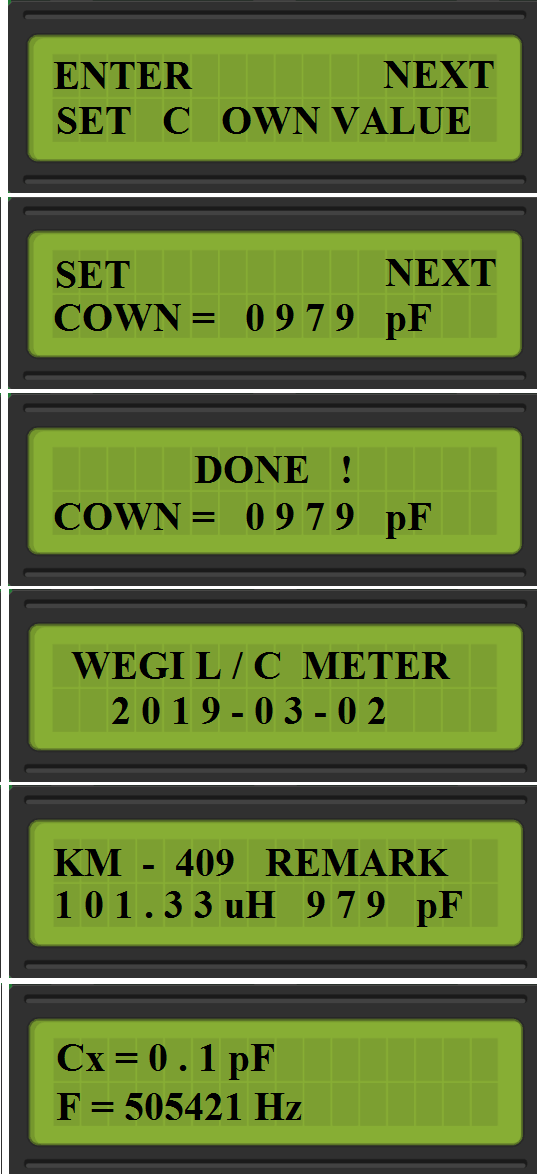
# MENU SET COWN VALUE: #
You can change the value of capacitor in LC generator circuit, after this the coil value will be recalculated.
**In the last 4 menu you can set the value by pressing left button and right button for confirm.**
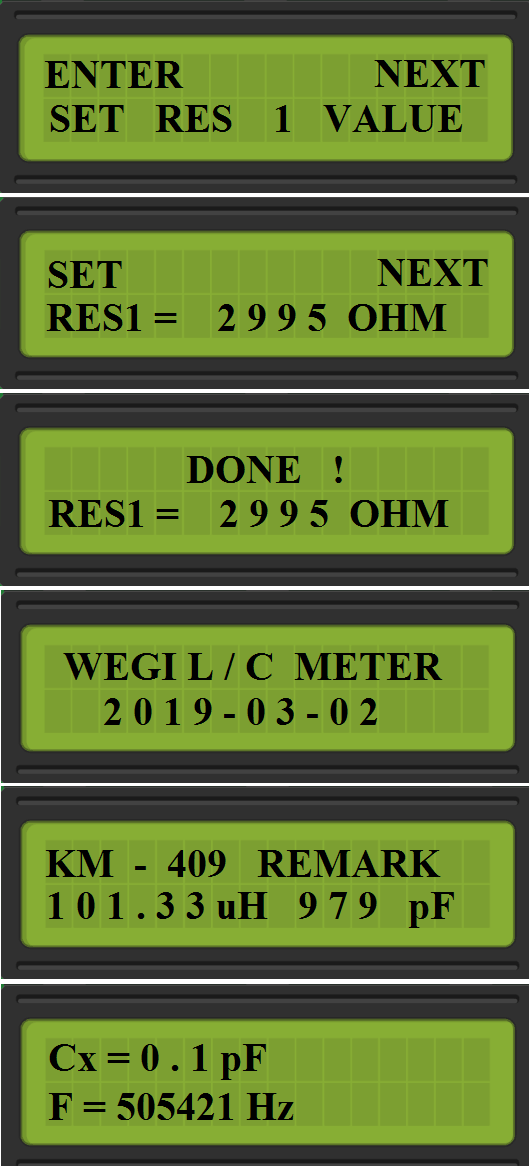
# MENU SET RES1 VALUE: #
Here you should set the RES1 value, which you measured after soldered RES1.
# MENU SET RES2 VALUE: #
Here you should set the RES2 value, which you measured after soldered RES2.
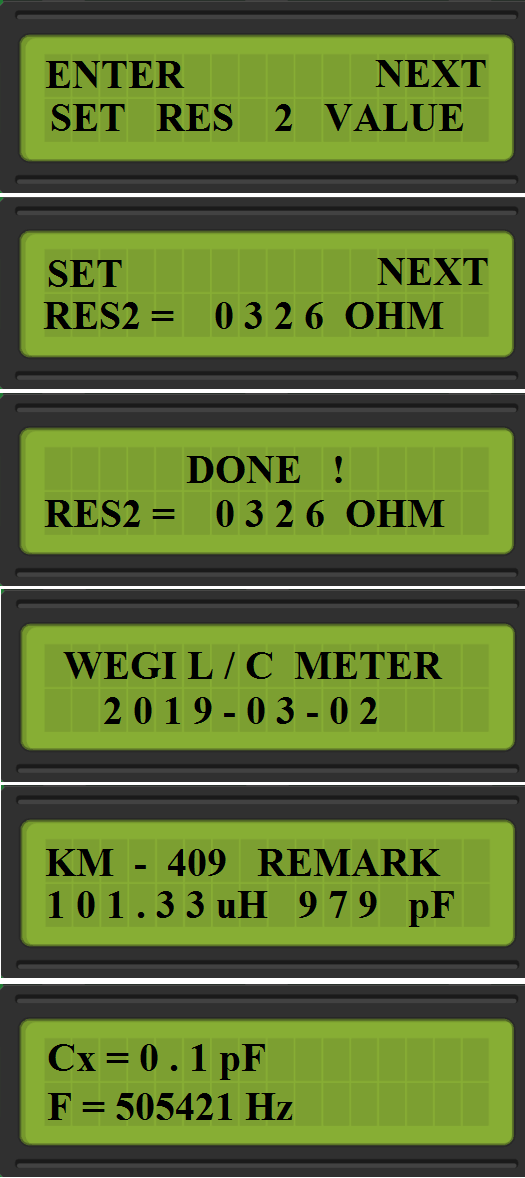
# ADDITIONS and CURIOS #
A bit unrolling the second one formula for clarity and understand how to do it on the integers numbers.
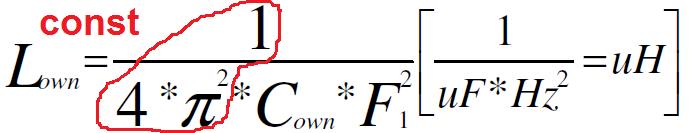
We got here a constant 1/4PI^2, also we dividing by [pF] so we can do sth like that:
100 000 000 000 000 000 000/4/Pi/Pi = 2 533 029 591 058 444 286
And now:
2 533 029 591 058 444 286 /F1/F1/C
**BECAUSE the 2 533 029 591 058 444 286 value is oversized by a few decades the result is in 0.01 [uH] what gave resolution in 10 [nH].**
Just for example how program calculate Cx or Lx and don’t going to to lower values using integers:
Cx = (Cown x [(F1 x F1)-(F2 x F2)])/F2/F2
So the first result = (Cown x [(F1 x F1)-(F2 x F2)]) is huge enough to divide by square of F2…
# KNOWN PROBLEMS: #
C9 10uF doesn’t work properly, breaking oscillations – solution – replaced to unpolarized
LM393D damaged under soldering probably – breaking oscillations – replaced to new.
eot
Design Drawing
schematic diagram
(
1
/
)
PCB
(
1
/
)
The preview image was not generated, please save it again in the
editor.
| ID | Name | Designator | Footprint | Quantity |
|---|---|---|---|---|
| 1 | LL4148 | D2 | LL-34 | 1 |
| 2 | 100nF | C3,C4,C5 | 1206 | 3 |
| 3 | LM7805CT | U1 | TO-220_HORIZONTAL | 1 |
| 4 | 1000u | C1 | CAP-D13.0XF5.0 | 1 |
| 5 | 100u | C2 | CAP | 1 |
| 6 | 10u | C9 | CASE-A_3216 | 1 |
| 7 | BC847 | Q3,Q4 | SOT-23(SOT-23-3) | 2 |
| 8 | 16x2 LCD (HD44780) | U4 | LCD1602 | 1 |
| 9 | 10k | PR1,PR2,PR3 | HELITRIM 329Y | 3 |
| 10 | 10uH | L1 | AXIAL-0.4 | 1 |
| 11 | 100uH | L2 | AXIAL-0.4 | 1 |
| 12 | BC857 | Q1 | SOT-23(SOT-23-3) | 1 |
| 13 | 8MHz | X1 | HC-49S | 1 |
| 14 | BUZZERHMB1275-12B | BUZZER1 | DIP-BUZZER-12X7.5 | 1 |
| 15 | 100n | C6 | 1206 | 1 |
| 16 | 33p | C7,C8 | 1206 | 2 |
| 17 | 1nF 2% | C11 | RAD-0.1 | 1 |
| 18 | 470nF | C10 | RAD-0.1 | 1 |
| 19 | POWERSUPPLY_DC21MMX | G$1 | POWERSUPPLY_DC-21MM | 1 |
| 20 | 2W10 | D1 | BRIDGE-WOB | 1 |
| 21 | ISP | P1 | HDR-IDC-2.54-2X3P | 1 |
| 22 | 1M | R1 | 1206 | 1 |
| 23 | 100k | R2,R3,R4 | 1206 | 3 |
| 24 | 10k | R5,R6 | 1206 | 2 |
| 25 | 2.2k | R7 | 1206 | 1 |
| 26 | 4.7k | R8,R9,R15 | 1206 | 3 |
| 27 | 3k | R11 | 1206 | 1 |
| 28 | 300 | R12 | 1206 | 1 |
| 29 | 1k | R13 | 1206 | 1 |
| 30 | SWITCH-MOMENTARYPTH | S1,S2 | TACTILE-PTH | 2 |
| 31 | HK19F-DC_5V-SHG | K2 | HK19F-DC5V-SHG(REAL) | 1 |
| 32 | Listwa ARK2 | U5,U6 | LISTWA ARK2 | 2 |
| 33 | MEGA8-P | U3 | DIP28-300 | 1 |
| 34 | LM393D | U2 | SOIC-8_150MIL | 1 |
Unfold
Project Members
Related Projects
Change a batch
Loading...
Add to album
×
Loading...
reminder
×
Do you need to add this project to the album?










